TETRAHEDRAL NUMBERS SERIES:
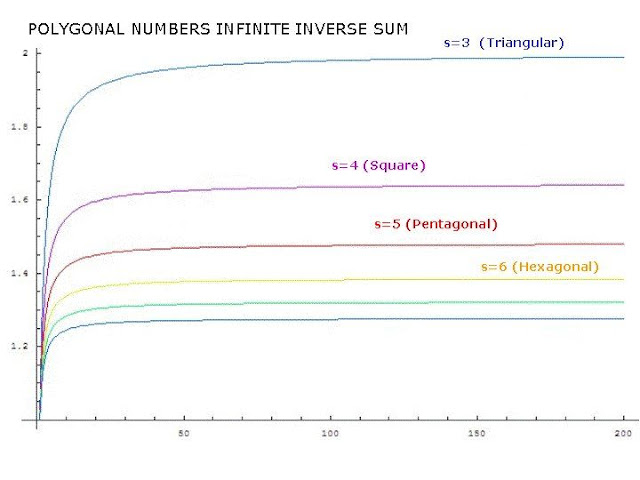
This post follows with the exercises on special numbers reciprocals related series, after the blog entries about Square Pyramidal Numbers and Polygonal Numbers . In fact, this example it is not very much interesting, but I wanted to write it before to deal with more difficult problems.
$latex \displaystyle T_{n}=\frac{n(n+1)(n+2)}{6}=\binom{n+2}{3}$
$latex \displaystyle S(n)=\sum_{k=1}^{n}{\frac{1}{T_{k}}=\sum_{k=1}^{n}{\frac{6}{k(k+1)(k+2)}$
If we split the main fraction into others:
$latex \displaystyle \frac{S(n)}{6}=\sum_{k=1}^{n}{\frac{1}{k(k+1)(k+2)}}=\sum_{k=1}^{n}{\left( \frac{A}{k}+\frac{B}{k+1}+\frac{C}{k+2} \right) }$
Solving the linear system of equations it gives:
$latex \displaystyle A=\frac{1}{2} \; ; B=-1 \; ; C=\frac{1}{2};$
This three series can be summed easily with the aid of the Harmonic Numbers:
$latex \displaystyle \sum_{k=1}^{n}{\frac{1}{k}=1+\frac{1}{2}+\frac{1}{3}+ \cdots +\frac{1}{n}=H_n$
$latex \displaystyle \sum_{k=1}^{n}{\frac{1}{k+1}=\frac{1}{2}+\frac{1}{3}+ \cdots +\frac{1}{n}+\frac{1}{n+1}=H_n-1+\frac{1}{n+1}$
$latex \displaystyle \sum_{k=1}^{n}{\frac{1}{k+2}=\frac{1}{3}+\frac{1}{4}+ \cdots +\frac{1}{n}+\frac{1}{n+1}+\frac{1}{n+2}=H_n-1-\frac{1}{2} + \frac{1}{n+1}+\frac{1}{n+2}$
If we substitute everything in the expression for the reciprocals sum:
$latex \displaystyle \frac{S(n)}{6}=\frac{n}{n+1}-\frac{1}{2}-\frac{1}{4} +\frac{1}{2(n+1)}+\frac{1}{2(n+2)}$
In the previous step we can see what does exactly means to be a "telescoping series", the term $latex H_n$, has vanished and there is no need to handle Euler Mascheroni Gamma and Digamma Function:
$latex H_{n}=\gamma + \psi_{0}(n+1)$
Then the formula for the n-th partial sum is:
$latex \displaystyle S(n)=\frac{3n(3+n)}{2(1+n)(2+n)}$
And evaluating the limit we get:
$latex \displaystyle S(\infty)=\lim_{n \leftarrow \infty}{S(n)}=\frac{3}{2}$
References:
[1]-Tetrahedral Number at- Wikipedia
[2]-Weisstein, Eric W. "Tetrahedral Number." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/TetrahedralNumber.html
[3] A000292-Tetrahedral (or pyramidal) numbers: C(n+2,3) = n(n+1)(n+2)/6. The On-Line Encyclopedia of Integer Sequences!