 BEHAVIOR OF THE PERCENTAJE OF TRAILING ZEROS IN THE DECIMAL EXPANSION OF n!
It was many and many a year ago, In a kingdom by the sea
BEHAVIOR OF THE PERCENTAJE OF TRAILING ZEROS IN THE DECIMAL EXPANSION OF n!
It was many and many a year ago, In a kingdom by the sea , I spent a very good time reading an spanish translation of Martin Gardner´s
"Mathematical Magic Show" [1] , just because
Annabel was not very much interested on me.
In this compilation from
Scientific American, Gardner dedicated some pages to this topic in an article called
"Factorial Oddities".
Gardner explained how, as $latex n$ increases, $latex n!$ is having more and more factors including the prime factor $latex 5$, that with other factors with any $latex 2$ it gives $latex 10$´s that accumulates in the decimal expansion of $latex n!$ creating a long tail of zeros [2] that fill the least significant digits of this kind of huge numbers.
As it is possible to calculate this number of
trailing zeros without having to expand the whole factorial, I wondered (when I was sixteen) if this final zeros were giving very much information about the digits of the whole factorial number or not.
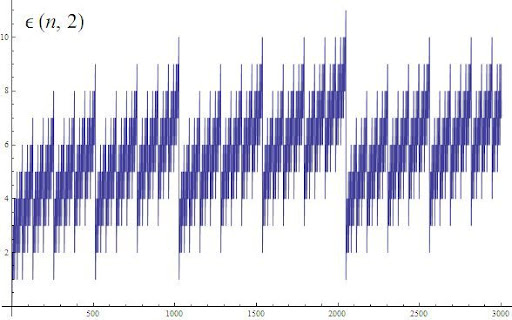
To answer this question, it is necessary to study the behaviour of $latex PTZ(n)$ the percentage between the trailing zeros and the total number of digits of $latex n!$ when $latex n$ tends to infinity.
Number of Digits of n!: [3]
$latex \displaystyle D_{10}(n!)=1+\lfloor log_{10}(n!) \rfloor$
Exponent of p in the prime factorization of n!: (Legendre´s formula)
$latex \displaystyle\alpha(n,p)=\sum _{i=1}^{\lfloor log_p(n)\rfloor}{ \bigg\lfloor\frac{n}{p^i} \bigg\rfloor $
Number of Trailing Zeros in n!. (See sequence
[2])
$latex NTZ(n!)=\alpha(n,5) $
PTZ(n!) = Percentage of trailing zeros of the total digits in n! (%)
$latex \displaystyle PTZ(n!)=100*\frac{NTZ(n!)}{D_{10}(n!)}$
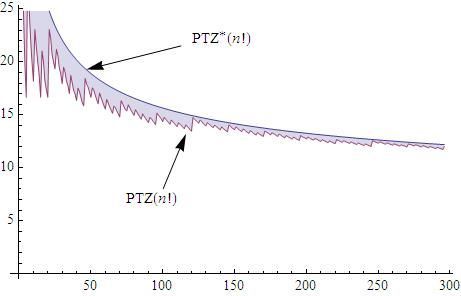
But if we want to test the limit of $latex PTZ(n)$ we need to work more handy bounds of this functions, notated with an added asterisk, and that they are going to hold for:
$latex \displaystyle D_{10}^{*}(n!) < D_{10}(n!)$
$latex \displaystyle NTZ^{*}(n!) \ge NTZ(n!)$
$latex \displaystyle PTZ^{*}(n!) > PTZ(n!)$
Approximation for the Number of Digits of n!:
We can sustitute the famous
Stirling's approximation instead of $latex n!$ in the formula for $latex D_{10}(n!)$:
$latex \displaystyle n! \approx \sqrt{2\pi n} \left({\frac{n}{e}\right)}^n$
$latex \displaystyle D_{10}(n!)=\left\lfloor \frac{-n+\left(n+\frac{1}{2}\right) \log (n)+\frac{1}{2} \log (2 \pi )}{\log (10)}\right\rfloor +1 +\delta_{n,1}$
The last formula gives the exact value for the number of digits of $latex n!$, for $latex n>0$, because the error for the Stirling´s formula is $latex O\left(\frac{1}{n}\right)$
But for our purposes we must make some changes inside $latex D_{10}(n)$ to get a continuous lower bound:
$latex \displaystyle D_{10}^{*}(n!)=\frac{-n+\left(n+\frac{1}{2}\right) \log (n)+\frac{1}{2} \log (2 \pi )}{\log (10)} < D_{10}(n)$
Approximation for the Legendre's formula and for the Number of Trailing Zeros:
$latex \displaystyle\alpha(n,p)= \sum _{i=1}^{\lfloor log_p(n)\rfloor} { \bigg\lfloor\frac{n}{p^i} \bigg\rfloor = \sum _{i=1}^{\infty} { \bigg\lfloor\frac{n}{p^i} \bigg\rfloor \leq \bigg\lfloor\sum _{i=1}^{\infty}{\frac{n}{p^i}}\bigg\rfloor =\bigg\lfloor \frac{n}{p-1}\bigg\rfloor =\alpha^{*}(n,p)$
$latex NTZ^{*}(n!) =\frac{n}{4} \ge \bigg\lfloor \frac{n}{4}\bigg\rfloor = \alpha^{*}(n,5) \ge \alpha(n,5)=NTZ(n!)$
Final Result and Limit:
$latex \displaystyle PTZ(n!)\approx PTZ^{*}(n!)=100*\frac{NTZ^{*}(n!)}{D_{10}^{*}(n!)}$
$latex \displaystyle\lim_{n \to{+}\infty}{PTZ^{*}(n!)}=0$
$latex PTZ(n!)$ is always positive and it is upper bounded by a continuous function that tend to zero as $latex n$ tends to infinity.
So the number of trailing zeros of $latex n!$ is giving lesser information about the decimal digits of $latex n!$ when the more grows $latex n$
This result may not cause any surprise, but long time ago I had a lot of fun when I was able to prove and plot it.
This ideas does not finish here, but on the contrary there are many many things than can be derived from this introductory point, and that are going to be material for further development in this blog.
References: [1]-Gardner, M. "Factorial Oddities." Ch. 4 in Mathematical Magic Show: More Puzzles, Games, Diversions, Illusions and Other Mathematical Sleight-of-Mind from Scientific American. New York: Vintage, pp. 50-65, 1978
[2]-A027868-Number of trailing zeros in n! The On-Line Encyclopedia of Integer Sequences!
[3]-A055642-Number of digits in decimal expansion of n. The On-Line Encyclopedia of Integer Sequences!
[5]-Trailing Zero @ Wikipedia
[6]-Stapel, Elizabeth. "Factorials and Trailing Zeroes." Purplemath. Available from
http://www.purplemath.com/modules/factzero.htm
[7]-A061010-Number of digits in (10^n)!. The On-Line Encyclopedia of Integer Sequences!
Archives:
[a]-121209-Number of Trailing Zeros of n!.nb